Weekly outline
-
Διδάσκων: Θεόδουλος Γαρεφαλάκης
Ώρες Γραφείου: Τρίτη 11:00 - 13:00 (Γ216)
Ώρες Μαθημάτων: Δευτέρα 11:00 - 13:00, Παρασκευή 11:00 - 13:00 (A201)
Ώρες Εργαστηρίων: Πέμπτη 15:00 - 17:00 (Ε212)
Συνιστούμε ισχυρά να παρακολουθείτε τις διαλέξεις και να συμμετέχετε στα εργαστήρια. Λύνοντας ασκήσεις στην διάρκεια του εξαμήνου είναι ο καλύτερος τρόπος αφενός να μάθετε και αφετέρου να εξασκηθείτε για τις εξετάσεις του μαθήματος.
Βαθμολογικό Σύστημα:
\(\)Θα γίνει μία πρόοδος περίπου στα μέσα του εξαμήνου και μία τελική εξέταση στην εξεταστική περίοδο του Ιανουαρίου. Εάν ο βαθμός της προόδου είναι $\Pi$ και ο βαθμός της τελικής εξέτασης είναι $Τ$, τότε ο βαθμός του μαθήματος υπολογίζεται ως\[ B = \max\{ 0.3\cdot \Pi + 0.7\cdot T, T\}\]
Για να περάσετε το μάθημα είναι απαραίτητο ο βαθμός $T$ της τελικής εξέτασης να είναι τουλάχιστον $4$ (και βέβαια ο συνολικός βαθμός $B$ να είναι τουλάχιστον $5$). Ο βαθμός της προόδου δεν μετράει στην εξέταση του Σεπτεμβρίου (εφόσον χρειαστεί να εξεταστείτε το Σεπτέμβρη).
Βιβλιογραφία:
- Σημειώσεις Χ. Κουρουνιώτη
- Μία εισαγωγή στην Γραμμική Άλγεβρα", Βάρσος, Δεριζιώτης, Εμμανουήλ, Μαλιάκας, Μελάς, Ταλλέλη
- "Γραμμική Άλγεβρα", Θεοχάρη-Αποστολίδη, Βαβατσούλας, Χαραλάμπους
- "Γραμμική Άλγεβρα και Εφαρμογές", G. Strang
- "Μια εισαγωγή στην Γραμμική Άλγεβρα", A. Morris
- "Μια εισαγωγή στην Γραμμική Άλγεβρα για τις θετικές επιστήμες", Χαραλάμπους, Φωτιάδης
- "Γραμμική Άλγεβρα", Μπεληγιάννης
-
Forum
-
Forum
-
Folder
-
\(\)Ορίσαμε την έννοια του $m\times n$ πίνακα ($m$ γραμμές και $n$ στήλες) επί του $\mathbb{R}$ και συμβολίσαμε το σύνολο τους με $\mathrm{Mat}_{m\times n}(\mathbb{R})$. Ονομάσαμε ένα πίνακα τετραγωνικό όταν $n=m$ και συμβολίσαμε το σύνολο τους με $\mathrm{Mat}_n(\mathbb{R})$.
Είδαμε πότε ένας τετραγωνικός πίνακας ονομάζεται άνω (ή κάτω) τριγωνικός, διαγώνιος, συμμετρικός και αντισυμμετρικός. Είδαμε την έννοια του ανάστροφου ενός πίνακα $A$ (και τον συμβολίσαμε $A^t$).
Ορίσαμε τις πράξεις της πρόσθεσης πινάκων, του πολλαπλασιασμού αριθμού με πίνακα και πολλαπλασιασμού πινάκων και είδαμε τις βασικές τους ιδιότητες.
Ορίσαμε πότε ένας πίνακας είναι αντιστρέψιμος.
-
\(\)Είδαμε κάποιες βασικές ιδιότητες των αντιστρέψιμων πινάκων.
Είδαμε την μέθοδο της απαλοιφής Gauss σε τετραγωνικά συστήματα (αντίστοιχα σε τετραγωνικούς πίνακες). Παρατηρήσαμε τα παρακάτω για ένα συστημα με $n$ εξισώσεις και $n$ αγνώστους:
- Αν η απαλοιφή καταλήξει σε ένα πλήρες σύνολο οδηγών (δηλαδή σε $n$ οδηγούς), τότε το σύστημα έχει μοναδική λύση.
- Αν η απαλοιφή καταλήξει σε ένα σύνολο με λιγότερους από $n$ οδηγούς (δηλαδή στον άνω τριγωνικό πίνακα, στον οποίο καταλήγουμε, υπάρχουν μηδενικά στη διαγώνιο), τότε το σύστημα είτε είναι αδύνατο είτε έχει άπειρες λύσεις.
Είδαμε τη μέθοδο απαλοιφής Gauss σε συστήματα (πίνακες) οποιουδήποτε σχήματος και ορίσαμε την έννοια του κλιμακωτού πίνακα. Είδαμε πότε ένα σύστημα έχει μοναδική λύση, πότε έχει άπειρες λύσεις και πότε είναι αδύνατο.
Ορίσαμε τους στοιχειώδεις πίνακες:
- $E_{i_0, i_1}(\lambda)$, που προκύπτει από τον ταυτοτικό πίνακα εάν στην $i_0$ γραμμή προσθέσουμε $\lambda$ φορές την $i_1$ γραμμή και
- $P_{i_0,i_1}$, που προκύπτει από τον ταυτοτικό πίνακα εάν εναλλάξουμε τις γραμμές $i_0$ και $i_1$.
Αποδείξαμε ότι οι στοιχειώδεις πίνακες είναι αντιστρέψιμοι και υπολογίσαμε τους αντιστρόφους τους (οι οποίοι είναι επίσης στοιχειώδεις πίνακες).
-
\(\)Δύο πίνακες ονομάζονται γραμμοϊσοδύναμοι εάν ο ένας μπορεί να προκύψει από τον άλλο με στοιχεώδεις πράξεις γραμμών. Δείξαμε ότι αν δύο πίνακες $A,B$ είναι γραμμοϊσοδύναμοι, τότε ο $A$ είναι αντιστρέψιμος αν και μόνο αν ο $B$ είναι αντιστρέψιμος. Επίσης παρατηρήσαμε ότι εάν ένα πίνακας έχει μια μηδενική γραμμή, τότε δεν είναι αντιστρέψιμος.
Χρησιμοποιήσαμε τα παραπάνω αποτελέσματα για να δείξαμουμε ότι ένας πίνακας $A\in\mathrm{Mat}_n(\mathbb{R})$ είναι αντιστρέψιμος αν και μόνο αν ο άνω τριγωνικός πίνακας που προκύπτει με τη διαδιακασία της απαλοιφής Gauss έχει $n$ οδηγούς. Ως ειδικές περιπτώσεις αυτού του αποτελέσματος, είδαμε ένας άνω (ή κάτω) τριγωνικός πίνακας είναι αντιστρέψιμος αν και μόνο αν όλα τα στοιχεία της διαγωνίου είναι διαφορετικά του μηδενός.
Είδαμε τη διαδικασία Gauss-Jordan για να ελέγχουμε εάν ένας τετραγωνικός πίνακας είναι αντιστρέψιμος και εάν είναι να τον υπολογίζουμε.
Δείξαμε ότι για κάθε πίνακα $A\in\mathrm{Mat}_{m\times n}(\mathbb{R})$ υπάρχει ένας πίνακας μετάθεσης $P\in\mathrm{Mat}_{m}(\mathbb{R})$, ένας κάτω τριγωνικός πίνακας $L\in\mathrm{Mat}_{m}(\mathbb{R})$ (με 1 παντού στη διαγώνιο) και ένας κλιμακωτός πίνακας $U\in\mathrm{Mat}_{m\times n}(\mathbb{R})$, τέτοιοι ώστε $PA = LU$.
-
\(\)Είδαμε τον ορισμό του διανυσματικού χώρου και δώσαμε παραδείγματα. Αποδείξαμε τις πρώτες ιδιότητες των πράξεων που προκύπτουν από τα αξιώματα του δ.χ. Ορίσαμε τι σημαίνει ένα υποσύνολο ενός δ.χ. να είναι κλειστό ως προς τις πράξεις του δ.χ.
Δείξαμε ότι ένα μη κενό υποσύνολο ενός δ.χ. είναι υπόχωρος αν και μόνο αν είναι κλειστό ως προς τις πράξεις (κριτήριο υπόχωρου).
Ορίσαμε τον υπόχωρο που παράγει ένα υποσύνολο $S$ ενός διανυσματικού χώρου $V$ (τον οποίο συμβολίσαμε $\langle S\rangle$ και ονομάσαμε γραμμική θήκη του $S$). Είδικότερα,
\[ \langle S\rangle = \left\{\lambda_1 v_1 +\cdots + \lambda_n v_n\ :\ \lambda_1,\ldots,\lambda_n\in \mathbb{R}, v_1,\ldots,v_n\in V\right\}.\]
Αποδείξαμε κάποιες βασικές ιδιότητες της γραμμικής θήκης.
-
\(\)Ορίσαμε την έννοια της γραμμικής ανεξαρτησίας και είδαμε παραδείγματα.
Ορίσαμε την έννοια της βάσης ενός δ.χ. Είδαμε ότι κάθε δ.χ. έχει βάση, αλλά το αποδείξαμε μόνο για πεπερασμένα παραγόμενους δ.χ.
Έστω $V$ ένας πεπερασμένα παραγόμενος δ.χ., $S$ ένα γραμμικώς ανεξάρτητο υποσύνολο του και $T$ ένα (πεπερασμένο) παράγον υποσύνολο του. Αποδείξαμε ότι $|S| \leq |T|$. Ειδικότερα, δείξαμε ότι αν $S = \{v_1,\ldots, v_n\}$ και $T = \{w_1,\ldots, w_m\}$, τότε $n \leq m$ και υπάρχουν δείκτες $i_1,\ldots, i_n$, τέτοιοι ώστε το σύνολο $(T \cup S) \setminus \{w_{i_1},\ldots, w_{i_n}\}$ παράγει τον $V$.
Εφαρμόσαμε το προηγούμενο αποτέλεσμα για να δείξουμε ότι αν $\mathcal{B}_1, \mathcal{B}_2$ είναι δύο βάσεις του χώρου $V$, τότε $|\mathcal{B}_1| = |\mathcal{B}_2|$.
-
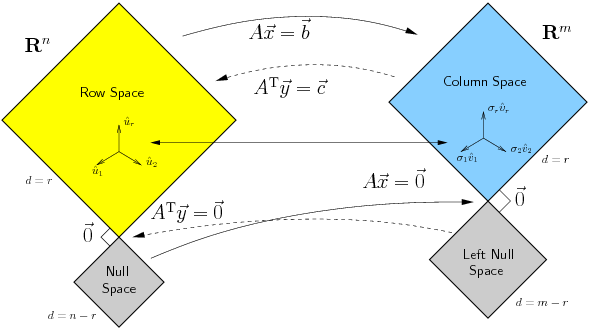
\(\)Ορίσαμε τους δύο βασικούς υπόχωρους ενός πίνακα $A\in \mathrm{Mat}_{m\times n}(\mathbb{R})$:
- Το μηδενόχωρο, $\mathcal{N}(A) = \left\{ x\in \mathbb{R}^n\ :\ Ax = 0\right\}$
- Το χώρο στηλών, $\mathcal{R}(A) = \langle A_1,\ldots, A_n\rangle$, όπου $A_1,\ldots,A_n$ είναι οι στήλες του πίνακα $A$.
Είδαμε πώς να υπολογίζουμε μία βάση για καθένα από τους παραπάνω χώρους. Επίσης, υπολογίσαμε τις διαστάσεις τους. Είδαμε ότι $\dim \mathcal{N}(A) = n - r$ και $\dim \mathcal{R}(A) = r$, όπου $r$ είναι το πλήθος των οδηγών μετά την απαλοιφή Gauss στον πίνακα $A$. Ο αριθμός $r$ εξαρτάται μόνο από τον πίνακα (και όχι από τη διαδικασία απαλοιφής) και ονομάζεται τάξη του πίνακα $A$. Τον συμβολίζουμε και $\mathrm{rank}(A)$.
Σε ένα χώρο διάστασης $n$ και ένα σύνολο $\mathcal{B}$ με $n$ διανύσματα τα παρακάτω είναι ισοδύναμα:
- Το σύνολο $\mathcal{B}$ είναι βάση
- Το σύνολο $\mathcal{B}$ είναι γραμμικώς ανεξάρτητο
- Το σύνολο $\mathcal{B}$ παράγει το χώρο
Είδαμε το χώρο γραμμών ενός πίνακα και πώς βρίσκουμε μία βάση του. Δείξαμε ότι η διάσταση του χώρου γραμμών είναι ίση με τη διάσταση του χώρου στηλών (και ίση με την τάξη του πίνακα).
-
\(\)Για δοσμένους υπόχωρους $X,Y$ ενός διανυσματικού χώρου $V$, είξαμε ότι η τομή τους $X \cap Y$ είναι υπόχωρος του $V$.
Oρίσαμε το άθροισμα τους
\[ X + Y = \left\{x + y\ :\ x\in X, y\in Y\right\}.\]
Ονομάσαμε το άθροισμα ευθύ εάν $X\cap Y = \{0\}$ και το συμβολίσαμε $X \oplus Y$.
Αποδειξαμε ότι
\[ \dim X + Y = \dim X + \dim Y - \dim X\cap Y.\]
-
-
\(\)Ορίσαμε την έννοια της γραμμικής απεικόνισης, είδαμε παραδείγματα και κάποιες βασικές ιδιότητες.
Δεδομένης μίας γραμμικής απεικόνισης $L : V \rightarrow W$, και υπόχωρων $X\leq V$, $Y\leq W$, ορίσαμε την εικόνα του $X$
\[ L(X) = \left\{w\in W\ :\ \exists x\in X, w = L(x)\right\} = \left\{L(x)\ :\ x \in X\right\}\]
και την αντίστροφη εικόνα του $Y$
\[ L^{-1}(Y) = \left\{v\in V\ :\ L(v)\in Y\right\}. \]
Αποδείξαμε ότι το $L(X)$ είναι υπόχωρος του $V$ και το $L^{-1}(Y)$ είναι υπόχωρος του $W$.
Ειδικές περιπτώσεις των παραπάνω είναι η εικόνα της $L$,
\[ \mathrm{im} L = \left\{ L(v)\ :\ v\in V\right\} \]
και ο πυρήνας της $L$
\[ \mathrm{ker} L = \left\{ v\in V\ :\ L(v) = 0\right\}. \]
Δείξαμε ότι για κάθε γραμμική απεικόνιση $L : \mathbb{R}^n \rightarrow \mathbb{R}^m$ υπάρχει πίνακας $A\in\mathrm{Mat}_{m\times n}(\mathbb{R})$ τέτοιος ώστε $L(x) = Ax$ για κάθε $x\in \mathbb{R}^n$ και είδαμε πώς να υπολογίζουμε τον πίνακα $A$.
Ορίσαμε τις έννοιες του μονομορφισμού, του επιμορφισμού και το ισομορφισμού.
Αποδείξαμε ότι αν $L : V \rightarrow W$ είναι ισομορφισμός, τότε υπάρχει μία μοναδική απεικόνιση, την οποία συμβολίσαμε με $L^{-1}$, η οποία είναι γραμμική και ικανοποιεί τις σχέσεις: $L\circ L^{-1} = \mathrm{id}_W$ και $L^{-1}\circ L = \mathrm{id}_V$. Η απεικόνιση $L^{-1}$ ονομάζεται αντίστροφη της $L$.
Έστω μία γραμμική απεικόνιση $L : V\rightarrow W$. Αποδείξαμε τα παρακάτω:
- Η $L$ είναι μονομορφισμός αν και μόνο αν $\mathrm{ker} L = \{0\}$.
- Η $L$ είναι επιμορφισμός αν και μόνο αν $\mathrm{im} L = W$.
Δείξαμε ότι μια γραμμική απεικόνιση $L : V\rightarrow W$ ορίζεται εάν δοθούν οι τιμές των στοιχείων μίας βάσης $\mathcal{B}$ του $V$. Με άλλα λόγια, εάν δοθούν οι τιμές $L(v_1),\ldots, L(v_n)$, όπου $\{v_1,\ldots,v_n\}$ είναι μία βάση του $V$, τότε έχουν καθοριστεί όλες οι τιμές της $L$.
-
\(\)Έστω $V,W$ διανυσματικοί χώροι πεπερασμένης διάστασης και $L: V\rightarrow W$ μία γραμμική απεικόνιση. Αποδείξαμε ότι
\[ \dim \ker(L) + \dim \mathrm{im}(L) = \dim V.\]
Δείξαμε ότι δύο χώροι πεπερασμένης διάστασης είναι ισόμορφοι αν και μόνο αν έχουν την ίδια διάσταση.
Δεδομένου χώρου $V$ διάστασης $n$ και μίας βάσης $\mathcal{B}=\{v_1,\ldots,v_n\}$ του $V$, ένας ισομορφισμός μεταξύ του $V$ και του $\mathbb{R}^n$ είναι η απεικόνιση που δίνει τις συντεταγμένες ώς προς τη βάση $\mathcal{B}$, δηλαδή η απεικόνιση
\[ \iota_{\mathcal{B}}: V \rightarrow \mathbb{R}^n,\ \ \ \iota_{\mathcal{B}}\left(\sum_{i=1}^n x_i v_i\right) = (x_1,\ldots, x_n)\]
Για την τιμή $\iota_{\mathcal{B}}(v)$ θα χρησιμοποιούμε και το συμβολισμό $[v]_{\mathcal{B}}$.
Δεδομένων χώρων $V, W$ και βάσεων τους $\mathcal{A}, \mathcal{B}$ αντίστοιχα και μίας γραμμικής απεικόνισης $L: V\rightarrow W$, ορίσαμε τον πίνακα της $L$ ως προς τις βάσεις $\mathcal{A}$ και $\mathcal{B}$ και τον συμβολίσαμε με $[L]_{\mathcal{A}}^{\mathcal{B}}$.
Δείξαμε ότι για κάθε $v\in V$ έχουμε $[L(v)]_{\mathcal{B}} = [L]_{\mathcal{A}}^{\mathcal{B}}\cdot [v]_{\mathcal{A}}$.
Είδαμε το χώρος των γραμμικών απεικονίσεων $L: V\rightarrow W$ και τον συμβολίσαμε με $\mathcal{L}(V, W)$. Αποδείξαμε ότι η απεικόνιση
\[ \theta: \mathcal{L}(V,W) \rightarrow \mathrm{Mat}_{m\times n}(\mathbb{R}),\ \ L\mapsto [L]_{\mathcal{A}}^{\mathcal{B}}\]
είναι ισομορφισμός, όπου $m = \dim W, n = \dim V$.
-
\(\)Έστω γραμμικές απεικονίσεις $L: V\rightarrow U$ και $T: U\rightarrow W$ και οι βάσεις $\mathcal{A}, \mathcal{B}, \mathcal{C}$ των χώρων $V, U, W$ αντίστοιχα. Δείξαμε ότι
\[ [T\circ L]_{\mathcal{A}}^{\mathcal{C}} = [T]_{\mathcal{B}}^{\mathcal{C}} \cdot [L]_{\mathcal{A}}^{\mathcal{B}} .\]
Μελετήσαμε ειδικά την ταυτοτική απεικόνιση $\mathrm{id}: V\rightarrow V$ με δύο δεδομένες βάσεις $\mathcal{A}, \mathcal{B}$ του χώρου $V$. Σύμφωνα με όσα έχουμε πει, ο πίνακας $[\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}}$ έχει την ιδιότητα
\[ [v]_{\mathcal{B}} = [\mathrm{id}(v)]_{\mathcal{B}} = [\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}} \cdot [v]_{\mathcal{A}}.\]
Ονομάσαμε τον πίνακα $[\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}}$ πίνακα αλλαγής βάση (από τη βάση $\mathcal{A}$ στη βάση $\mathcal{B}$).
Δείξαμε ότι μία γραμμική απεικόνιση $L: V\rightarrow U$ είναι ισομορφισμός αν και μόνο αν ο πίνακας $[L]_{\mathcal{A}}^{\mathcal{B}}$ είναι αντιστρέψιμος, όπου $\mathcal{A}$ και $\mathcal{B}$ είναι βάσεις των $V, U$ αντίστοιχα. Μάλιστα, όταν η $L$ είναι ισομορφισμός, ισχύει $[L^{-1}]_{\mathcal{B}}^{\mathcal{A}} = ([L]_{\mathcal{A}}^{\mathcal{B}})^{-1}$.
Ειδικότερα, για την ταυτοτική απεικόνιση, αυτό σημαίνει ότι $[\mathrm{id}]_{\mathcal{B}}^{\mathcal{A}} = ([\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}})^{-1}$.
Είδαμε παραδείγματα.
Είδαμε τον ορισμό της οριζουσιακής απεικόνισης και δείξαμε αρκετές ιδιότητες που προκύπτουν από αυτόν. Είδαμε ότι για κάθε φυσικό αριθμό $n$ υπάρχει μοναδική απεικόνιση $\mathrm{det}: \mathrm{Mat}_n(\mathbb{R}) \rightarrow \mathbb{R}$ που να ικανοποιεί τις τρεις ιδιότητες της οριζουσιακής απεικόνισης.
Είδαμε παραδείγματα υπολογισμού οριζουσών.
-
\(\)Αποδείξαμε περισσότερες ιδιότητες της ορίζουσας. Ειδικότερα, δείξαμε ότι $\mathrm{det}(A\cdot B) = \mathrm{det}(A)\cdot \mathrm{det}(B)$ και $\mathrm{det}(A^t) = \mathrm{det}(A)$.
Είδαμε παραδείγματα υπολογισμού οριζουσών.
-
Λύσαμε ασκήσεις.
-
-