Weekly outline
-
Διδάσκων: Θεόδουλος Γαρεφαλάκης
Ώρες διαλέξεων: Δευτέρα και Τετάρτη 9:00 - 11:00 (αίθουσα Α208, κτίριο ΤΜΕΜ)
Ώρες γραφείου: Δευτέρα και Τετάρτη 11:00 - 13:00 (γραφείο Γ216, κτίριο ΤΜΕΜ)
Περιεχόμενο του μαθήματος: Εδώ μπορείτε να δείτε το περιεχόμενο του μαθήματος (και σε αρχείο pdf).
\(\)Βαθμολογικό σύστημα: Κατά τη διάρκεια του εξαμήνου θα σας δοθούν κάποια φυλλάδια ασκήσεων, από τα οποία θα πρέπει να λύσετε και να παραδώσετε κάποιες ασκήσεις. Επίσης, θα γίνει μία πρόοδος και θα γίνει και μία τελική εξέταση. Ο τελικός σας βαθμός θα υπολιστεί ως εξής:
\[ Β = \max\{0.3 \cdot Α + 0.2\cdot Π + 0.5\cdot Τ, 0.2\cdot Π + 0.8\cdot Τ, 0.3\cdot Α + 0.7\cdot Τ, Τ\} \]
όπου $Α$ είναι ο μέσος όρος των βαθμών των ασκήσεων, $Π$ είναι ο βαθμός της προόδου και $Τ$ είναι ο βαθμός της τελικής εξέτασης.
Βιβλιογραφία:
- Σημειώσεις Χ. Κουρουνιώτη
- Μια εισαγωγή στην Γραμμική Άλγεβρα για τις θετικές επιστήμες, Χαραλάμπους, Φωτιάδης
- Γραμμική Άλγεβρα και Εφαρμογές, G. Strang
- Μία εισαγωγή στην Γραμμική Άλγεβρα, Βάρσος, Δεριζιώτης, Εμμανουήλ, Μαλιάκας, Μελάς, Ταλλέλη
- Γραμμική Άλγεβρα, Θεοχάρη-Αποστολίδη, Βαβατσούλας, Χαραλάμπους
- Μια εισαγωγή στην Γραμμική Άλγεβρα, A. Morris
- Γραμμική Άλγεβρα, Μπεληγιάννης
Τα επόμενα μαθήματα θα γίνουν 10 και 15 Ιανουαρίου. Η τελική εξέταση του μαθήματος θα γίνει την Παρασκευή 19 Ιανουαρίου, Παρασκευή 26 Ιανουαρίου, 10:00 - 12:00 στην αίθουσα Β201.
-
Forum
-
Forum
-
Folder
-
\(\)Είδαμε το σύνολο $\mathbb{R}^n$ (ονομάσαμε τα στοιχεία του "διανύσματα" μήκους $n$) και ορίσαμε δύο πράξεις:
1. πρόσθεση δύο διανυσμάτων
\[ (x_1,\ldots, x_n) + (y_1,\ldots, y_n) = (x_1+y_1,\ldots, x_n+y_n)\]
2. πολλαπλασιασμό αριθμού με διάνυσμα
\[ \lambda \cdot (x_1,\ldots, x_n) = (\lambda x_1, \ldots, \lambda x_n)\]
Είδαμε διάφορες ιδιότητες που ικανοποιούν οι πράξεις αυτές.
Είδαμε το σύνολο των $m\times n$ ($m$ επί $n$) πινάκων $\mathbb{R}^{m\times n}$. Ένας $m\times n$ πίνακας είναι μία διάταξη αριθμών σε $m$ γραμμές και $n$ στήλες. Συνήθως θα περιγράφουμε ένα τέτοιο πίνακα $A$ δίνοντας τα στοιχεία του $a_{ij}$ για $i=1,\ldots,m$, $j=1,\ldots,n$. Oρίσαμε δύο πράξεις αντίστοιχες με αυτές του $\mathbb{R}^n$:
1. πρόσθεση δύο πινάκων
\[ \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} &\cdots & a_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) + \left(\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1n} \\ a_{21} & b_{22} &\cdots & b_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \end{array} \right) = \left(\begin{array}{cccc} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\ a_{21} + b_{21} & a_{22} +b_{22} &\cdots & a_{2n} + b_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn} \end{array} \right) \]
2. πολλαπλασιασμό αριθμού με πίνακα
\[ \lambda \cdot \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} &\cdots & a_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) = \left(\begin{array}{cccc} \lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n} \\ \lambda a_{21} & \lambda a_{22} &\cdots & a_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ \lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn} \end{array} \right) \]
Είδαμε ότι οι πράξεις της πρόσθεσης πινάκων και του πολλαπλασιασμού αριθμού με πίνακα ικανοποιούν τις ίδιες ιδιότητες με αντίστοιχες πράξεις του $\mathbb{R}^n$.
Ορίσαμε τον πολλαπλασιασμό πινάκων. Ειδικότερα, όταν $A\in \mathbb{R}^{m\times p}$ και $B\in \mathbb{R}^{p\times n}$, (δηλαδή το πλήθος στηλών του $Α$ είναι ίσο με το πλήθος γραμμών του $B$) τότε ορίζεται το γινόμενο $A\cdot B$, το οποίο είναι ένας $m\times n$ πίνακας. To $i,j$ στοιχείο του πίνακα $AB$ είναι το
\[ (AB)_{ij} = \sum_{k = 1}^p A_{ik} B_{kj}.\]
Είδαμε βασικές ιδιότητες του πολλαπλασιασμού πινάκων.
Ορίσαμε πότε ένας τετραγωνικός πίνακας είναι αντιστρέψιμος.
Ορίσαμε τις έννοιες του άνω (κάτω) τριγωνικού πίνακα, του διαγώνιου πίνακα, του συμμετρικού και του αντισυμμετρικού πίνακα. Δεδομένου ενός πίνακα $A\in \mathbb{R}^{m\times n}$ ορίσαμε τον ανάστροφο πίνακα, $A^{\top}\in \mathbb{R}^{n\times m}$.
Δεδομένων δύο πινάκων $A\in \mathbb{R}^{m\times p},\ B\in \mathbb{R}^{p\times n}$, το γινόμενο τους $C = AB$ είναι ένας $m\times n$ πίνακας. Αν συμβολίσουμε με $\mathbf{a}_1, \ldots, \mathbf{a}_p$ τις στήλες του $A$, $\mathbf{c}_1, \ldots, \mathbf{c}_n$ τις στήλες του $C$ και $B_{ij}$ το στοιχείο του πίνακα $B$ στη θέση $i,j$, τότε μπορούμε να περιγράψουμε τις στήλες του πίνακα $C$ ως εξής:
\[ \mathbf{c}_j = \sum_{k=1}^p B_{k, j}\ \mathbf{a}_k\ \ \ \text{ για }\ \ j=1,\ldots,n.\]
Δηλαδή, η $j$ στήλη του $C$ είναι ο γραμμικός συνδυασμός των στηλών του $A$ με συντελεστές από την $j$ στήλη του $B$.
Παρόμοια μπορούμε να περιγράψουμε τις γραμμές του πίνακα $C$ ως γραμμικό συνδυασμό των γραμμών του πίνακα $B$. Ειδικότερα,
\[ C_i = \sum_{k=1}^p A_{i,k}\ B_k, \ \ \text{ για }\ \ i=1,\ldots,m, \]
όπου $B_k$ και $C_i$ είναι οι γραμμές των πινάκων $B$ και $C$ αντίστοιχα.
-
\(\)Είδαμε τι είναι ένα γραμμικό σύστημα $m$ εξισώσεων με $n$ αγνώστους:
\[ \left\{\begin{array}{ccccccccc} a_{11}\ x_1 &+& a_{12}\ x_2 &+& \cdots &+& a_{1n}\ x_n &=& b_1 \\ a_{21}\ x_1&+& a_{22}\ x_2&+&\cdots &+& a_{2n}\ x_n &=& b_2\\ \vdots & & \vdots & & \cdots& &\vdots& &\vdots\\ a_{m1}\ x_1&+& a_{m2}\ x_2&+& \cdots &+& a_{mn}\ x_n &=& b_m\end{array} \right\}\]
Ονομάσαμε τον πίνακα
\[ \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} &\cdots & a_{2n} \\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)\]
πίνακα του συστήματος και τον πίνακα
\[ \left(\begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} &\cdots & a_{2n} & b_2\\ \vdots & \vdots & \cdots &\vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m\end{array} \right) \]
επαυξημένο πίνακα του συστήματος.
Είδαμε την μέθοδο απαλοιφής Gauss για την λύση ενός γραμμικού συστήματος. Στόχος της απαλοιφής είναι να φέρει τον πίνακα σε κλιμακωτή μορφή. Στον κλιμακωτό πίνακα μπορεί να υπάρχουν μηδενικές γραμμές, οι οποίες βρίσκονται μετά τις μη μηδενικές γραμμές. Σε κάθε μη μηδενική γραμμή του κλιμακωτού πίνακα, το πρώτο από αριστερά μη μηδενικό στοιχείο ονομάζεται οδηγός.
Είδαμε ότι σε ένα $n \times n$ σύστημα, αν η απαλοιφή καταλήξει σε ένα κλιμακωτό πίνακα με $n$ οδηγούς, τότε οι οδηγοί βρίσκονται στη διαγώνιο του πίνακα και το σύστημα έχει μοναδική λύση που μπορεί να υπολογιστεί με ανάδρομη αντικατάσταση.
Παρατηρήσαμε ότι η απαλοιφή Gauss σε ένα $m\times n$ πίνακα οδηγεί σε ένα κλιμακωτό πίνακα με $r$ οδηγούς, όπου $r\leq m$ και $r\leq n$ (αυτό γράφεται πιο σύντομα και $r\leq \min\{m,n\}$).
-
\(\) Ολοκληρώσαμε την περιγραφή της μεθόδου απαλοιφής Gauss. Είδαμε ότι με απαλοιφή Gauss, κάθε πίνακας $A\in \mathbb{R}^{m\times n}$ καταλήγει σε κάποιο κλιμακωτό πίνακα $B$. Ο πίνακας αυτός δεν είναι μοναδικός: κάποιος που θα κάνει μια διαφορετική ακολουθία πράξεων γραμμών θα καταλήξει ενδεχομένως σε διαφορετικό κλιμακωτό πίνακα $B'$. Όμως οι πίνακες $B$ και $B'$ περιέχουν οδηγούς στις ίδιες ακριβώς στήλες (και συνεπώς το πλήθος των οδηγών είναι το ίδιο). Ονομάσαμε το πλήθος τον οδηγών τάξη του πίνακα $A$ και τη συμβολίσαμε $\mathrm{rank}(A)$.
Ονομάσαμε τις μεταβλητές που αντιστοιχούν σε στήλες με οδηγο βασικές ή δεσμευμένες και τις μεταβλητές που αντιστοιχούν σε στήλες χωρίς οδηγό ελεύθερες. Όταν το σύστημα δεν είναι αδύνατο, είδαμε ότι η ανάδρομη αντικατάσταση οδηγεί στη γενική λύση του συστήματος, η οποία τελικά είναι κάποιο σταθερό διάνυσμα σύν κάθε πιθανό γραμμικό συνδυασμό $n - \mathrm{rank}(A)$ διανυσμάτων (ένα διάνυσμα για κάθε ελεύθερη μεταβλητή). Αυτό μας οδήγησε στην παρατήρηση: σε ένα $m\times n$ σύστημα με πίνακα τάξης $r$ υπάρχουν τρεις περιπτώσεις:
- Το σύστημα είναι αδύνατο (καμία λύση)
- Το σύστημα έχει λύσεις και $r = n$ οπότε έχουμε μοναδική λύση
- Το σύστημα έχει λύσεις και $r < n$ οπότε έχουμε άπειρες λύσεις
Είδαμε πώς γράφεται ένα σύστημα ως εξίσωση πινάκων. Ειδικότερα, αν $A\in \mathbb{R}^{m\times n}$ είναι ο πίνακας του συστήματος, $B\in \mathbb{R}^m$ είναι το διάνυσμα του 2ου μέλους και $x\in \mathbb{R}^n$ είναι το διάνυσμα των μεταβλητών, τότε το σύστημα γράφεται ως $A\cdot x = b$.
Δείξαμε ότι ένας $n\times n$ πίνακας $A$ είναι αντιστρέψιμος αν και μόνο αν $\mathrm{rank}(A) = n$. Δηλαδή αν έχει, όπως λέμε, πλήρες σύνολο οδηγών. Σε αυτή την περίπτωση το σύστημα $A\cdot x = b$ έχει μοναδική λύση την $x = A^{-1}\cdot b$.
Είδαμε τη μέθοδο Gauss-Jordan για υπολογισμό του αντιστρόφου ενός πίνακα $A$ όταν είναι αντιστρέψιμος.
Είδαμε ότι οι πράξεις γραμμών σε ένα πίνακα $A\in \mathbb{R}^{m\times n}$ μπορούν να εκφραστούν ως γινόμενο κάποιου πίνακα, τον οποίο ονομάσαμε στοιχειώδη πίνακα, με τον πίνακα $A$. Υπάρχουν δύο ειδών στοιχειώδεις πίνακες:
- $E_{i,j}(\lambda) \in \mathbb{R}^{m\times m}$, για κάποια $1\leq i,j\leq m$ και $i\neq j$, και $\lambda\in \mathbb{R}$, ο οποίος προκύπτει από τον ταυτοτικό πίνακα αν αντικαταστήσουμε το 0 στη θέση $(i,j)$ με το $\lambda$. Ο πίνακας $B = E_{i,j}(\lambda) A$ προκύπτει από τον $A$ αν στη γραμμή $i$ του $A$ προσθέσουμε $\lambda$ φορές τη γραμμή $j$.
- $P_{i,j}\in \mathbb{R}^{m\times m}$, για κάποια $1\leq i,j\leq m$ και $i\neq j$, ο οποίος προκύπτει από τον ταυτοτικό πίνακα αν εναλλάξουμε τις γραμμές $i$ και $j$. Ο πίνακας $B = P_{i,j} A$ προκύπτει από τον $A$ αν εναλλάξουμε τις γραμμές $i$ και $j$ του $A$.
Είδαμε βασικές ιδιότητες των στοιχειωδών πινάκων και εκφράσαμε την απαλοιφή Gauss ως γινόμενο στοιχειωδών πινάκων με τον πίνακα $A$. Από αυτό καταλήξαμε σε πίνακες $P, L\in \mathbb{R}^{m\times m}$ και πίνακα $U\in \mathbb{R}^{m\times n}$ τέτοιους ώστε:
- Ο πίνακας $P$ είναι πίνακας μετάθεσης (προκύτει από τον ταυτοτικό εάν κάνω κάποιες εναλλαγές γραμμών).
- Ο πίνακας $L$ είναι κάτω τριγωνικός με 1 στη διαγώνιο.
- Ο πίνακας $U$ είναι ο κλιμακωτός πίνακας που προκύτπει από την απαλοιφή Gauss.
Δείξαμε ότι οι πίνακες $P, L$ είναι αντιστρέψιμοι.
-
\(\)Ορίσαμε την έννοια της οριζουσιακής απεικόνισης $\mathrm{det} : \mathbb{R}^{n\times n} \rightarrow \mathbb{R}$. Η ορίζουσα του πίνακα $A = (a_{ij}) \in \mathbb{R}^{n\times n}$ δίνεται από τον τύπο
\[ \mathrm{det}(A) = (-1)^{1+j}\ a_{1j}\ \mathrm{det}(A_{1j}) + (-1)^{2+j}\ a_{2j}\ \mathrm{det}(A_{2j}) + \cdots + (-1)^{i+j}\ a_{ij}\ \mathrm{det}(A_{ij}) + \cdots + (-1)^{n+j}\ a_{nj}\ \mathrm{det}(A_{nj}), \]
όπου $A_{ij}$ είναι ο ελάσσονας πίνακας του στοιχείου $a_{ij}$ (είναι ο $(n-1)\times (n-1)$ πίνακας που προκύπτει από τον $A$ αν διαγράψουμε την $i$ γραμμή και τη $j$ στήλη). Ο παραπάνω τύπος ονομάζεται και ανάπτυγμα της ορίζουσας ως προς την $j$ στήλη. Το αποτέλεσμα είναι το ίδιο ανεξάρτητα από τη στήλη ως προς την οποία θα πάρουμε το ανάπτυγμα.
Είδαμε βασικές ιδιότητες:
- $\mathrm{det}(r_1,\ldots,r_i'+\lambda r_i'',\ldots, r_n) = \mathrm{det}(r_1,\ldots,r_i',\ldots, r_n) + \lambda \mathrm{det}(r_1,\ldots,r_i'',\ldots, r_n)$,
- Αν δύο οποιεσδήποτε γραμμές ενός πίνακα $A$ είναι ίσες, τότε $\mathrm{det}(A) = 0$,
- $\mathrm{det}(I_n) = 1$,
- Αν ο πίνακας $B$ προκύπτει από τον πίνακα $A$ με εναλλαγή δύο γραμμών, τότε $\mathrm{det}(B) = -\mathrm{det}(A)$,
- Αν ο πίνακας $B$ προκύπτει από τον πίνακα $A$ αν στην $i$ γραμμή προσθέσουμε ένα πολλαπλάσιο της $j$ γραμμής, τότε $\mathrm{det}(B) = \mathrm{det}(A)$,
- \(\mathrm{det}(A\cdot B) = \mathrm{det}(A)\cdot \mathrm{det}(B)\),
- $\mathrm{det}(\lambda A) = \lambda^n \mathrm{det}(A)$,
- Αν ο πίνακας $A$ είναι άνω (ή κάτω) τριγωνικός, τότε η ορίζουσα του είναι ίση με το γινόμενο των στοιχείων της διαγωνίου.
- $\mathrm{det}(A^{\top}) = \mathrm{det}(A)$.
Ο ιδιότητες 4,5 μας δείχνουν ότι κατά την απαλοιφή Gauss οι διαδοχικοί πίνακες είτε έχουν είτε ίση ή αντίθετη ορίζουσα. Η ιδιότητα 8 μας επιτρέπει να υπολογίζουμε την ορίζουσα του άνω τριγωνικού πίνακα στον οποίο καταλήγουμε.
Η ιδιότητα 9 μας λέει ότι μπορούμε να αναπτύσουμε και ως προς γραμμές. Επίσης, μπορούμε να εφαρμόσουμε τις ιδιότητες 1, 2, 4, 5 για τις στήλες του πίνακα.
Είδαμε ότι για ένα πίνακα $A\in \mathbb{R}^{n\times n}$ ισχύει $\mathrm{det}(A) \neq 0$ αν και μόνο αν ο πίνακας $A$ είναι αντιστρέψιμος. Έτσι έχουμε τις ακόλουθες προτάσεις οι οποίες είναι ισοδύναμες:
- Ο πίνακας $A$ είναι αντιστρέψιμος.
- Η απαλοιφή Gauss στον πίνακα $A$ καταλήγει σε ένα άνω τριγωνικό πίνακα με $n$ οδηγούς.
- Το σύστημα $Ax=0$ έχει μόνο τη μηδενική λύση.
- $\mathrm{det}(A) \neq 0$.
Όταν ο πίνακας $A$ είναι αντιστρέψιμος, είδαμε ότι $A^{-1} = \frac{1}{\mathrm{det}(A)}\ \mathrm{adj}(A)$, όπου $\mathrm{adj}(A)$ είναι ο προσαρτημένος (adjoint) του $A$. Από αυτό οδηγούμαστε στον κανόνα του Cramer για επίλυση τετραγωνικών συστημάτων.
Είδαμε παραδείγματα υπολογισμού οριζουσών.
-
\(\)Ορίσαμε την έννοια του υπόχωρου $S$ ενός διανυσματικού χώρου $V$: είναι ένα μη κενό υποσύνολο του $V$ τέτοιο ώστε
- Για κάθε $u, v\in S$ έχουμε $u+v \in S$
- Για κάθε $v\in S$ και κάθε $\lambda \in \mathbb{R}$ έχουμε $\lambda v \in S$
Οι δύο παραπάνω συνθήκες μπορούν να γραφτούν ισοδύναμα: Για κάθε $u,v \in S$ και κάθε $\lambda \in \mathbb{R}$ έχουμε $\lambda v + u \in S$.
Με άλλα λόγια, ένα μη κενό υποσύνολο του $\mathbb{R}^n$ είναι υπόχωρος του αν είναι κλειστό ως προς τις πράξεις (πρόσθεσης και βαθμωτού πολλαπλασιασμού). Έτσι εάν πάρουμε διανύσματα $v_1,\ldots, v_m\in S$ και αριθμούς $\lambda_1,\ldots, \lambda_m\in \mathbb{R}$, τότε $\lambda_1\ v_1 + \cdots + \lambda_m\ v_m \in S$.
Είδαμε παραδείγματα υποσυνόλων που δεν είναι υπόχωροι. Είδαμε κάποιες γενικές κατασκευές υποχώρων. Ειδικότερα, εάν $v_1,\ldots, v_m \in \mathbb{R}^n$, τότε το σύνολο των γραμμικών συνδυασμών των διανυσμάτων $v_1,\ldots, v_m$, δηλαδή το
\[\mathrm{Span}(\{v_1,\ldots, v_m\}) = \left\{ \lambda_1\ v_1 + \cdots + \lambda_m\ v_m\ :\ \lambda_1,\ldots, \lambda_m\in \mathbb{R}\right\} \]
είναι υπόχωρος του $\mathbb{R}^n$ και ονομάζεται ο υπόχωρος που παράγεται από το σύνολο $\{v_1,\ldots, v_m\}$.
Είδαμε επίσης, ότι αν $A\in \mathbb{R}^{m\times n}$ τότε το σύνολο λύσεων του ομογενούς συστήματος $Ax = 0$ είναι υπόχωρος του $\mathbb{R}^n$.
Δείξαμε ότι αν $v \in \mathrm{Span}(\{v_1,\ldots, v_m\})$ , τότε $\mathrm{Span}(\{v_1,\ldots, v_m, v\}) = \mathrm{Span}(\{v_1,\ldots, v_m\})$ (δηλαδή αν το διάνυσμα $v$ ήδη ανήκει στον υπόχωρο που παράγουν τα $v_1,\ldots, v_m$, τότε αν το συμπεριλάβουμε στο παράγον σύνολο δεν παίρνουμε νέα διανύσματα. Ο υπόχωρος που παράγεται παραμένει ο ίδιος).
Δείξαμε ότι $\mathrm{Span}(\{v_1,\ldots, v_i, \ldots, v_j, \ldots, v_m\}) = \mathrm{Span}(\{v_1,\ldots, v_i, \ldots, v_j+\lambda v_i, \ldots, v_m\})$. Αυτό σημαίνει ότι ο χώρος που παράγουν οι γραμμές ενός πίνακα $A\in \mathbb{R}^{m\times n}$ δεν αλλάζει καθώς κάνουμε πράξεις γραμμών στον πίνακα $A$ (όπως κάνουμε στην απαλοιφή Gauss). Για παράδειγμα, αν πάρουμε τα διανύσματα $(1, 0, 1), (-1, 1, -2), (1, 1, 1), (0, 1, 2)\in \mathbb{R}^3$ και φτιάξουμε τον πίνακα
\[ \left(\begin{array}{rrr} 1& 0& 1\\ -1& 1&-2\\ 1& 1& 1\\ 0& 1& 2\end{array}\right)\]
και κάνουμε απαλοιφή Gauss καταλήγουμε στον πίνακα
\[\left(\begin{array}{rrr} 1& 0& 1\\ 0& 1& 1\\ 0& 0& -1\\ 0& 0& 0\end{array}\right).\]
Άρα $\mathrm{Span}(\{(1, 0, 1), (-1, 1, -2), (1, 1, 1), (0, 1, 2)\}) = \mathrm{Span}(\{(1,0,1), (0,1,1), (0,0,-1), (0,0,0)\})$ και καθώς το διάνυσμα $(0,0,0)$ δεν προσφέρει στους γραμμικούς συνδυασμούς, έχουμε
\[ \mathrm{Span}(\{(1, 0, 1), (-1, 1, -2), (1, 1, 1), (0, 1, 2)\}) = \mathrm{Span}(\{(1,0,1), (0,1,1), (0,0,-1)\}).\]
Παρατηρούμε ότι ο ίδιος υπόχωρος παράγεται από διαφορετικά σύνολα διανυσμάτων, τα οποία σύνολα, μπορεί να μη έχουν ούτε το ίδιο πλήθος διανυσμάτων. Στο παράδειγμα μας, ο χώρος γραμμών του αρχικού πίνακα παράγεται από τα τέσσερα διανύσματα $(1, 0, 1), (-1, 1, -2), (1, 1, 1), (0, 1, 2)$, αλλά επίσης παράγεται από τα τρία διανύσματα $(1,0,1), (0,1,1), (0,0,-1)$.
Ορίσαμε την έννοια της γραμμική εξάρτησης/ανεξαρτησίας ενός συνόλου διανυσμάτων του $\mathbb{R}^n$: Το σύνολο $\{v_1,\ldots, v_m\}$ είναι γραμμικώς εξαρτημένο εάν υπάρχουν πραγματικοί αριθμοί $\lambda_1,\ldots, \lambda_m$, όχι όλοι ίσοι με 0, τέτοιοι ώστε
\[ \lambda_1\ v_1 + \cdots + \lambda_m\ v_m = 0. \]
Το σύνολο $\{v_1,\ldots, v_m\}$ ονομάζεται γραμμικώς ανεξάρτητο εάν δεν είναι γραμμικώς εξαρτημένο, δηλαδή
\[ \lambda_1\ v_1 + \cdots + \lambda_m\ v_m = 0\ \ \Longrightarrow\ \ \lambda_1 = \cdots = \lambda_m = 0.\]
Με άλλα λόγια είναι γραμμικώς ανεξάρτητο εάν ο μοναδικός τρόπος να γράψει κανείς το 0 ως γραμμικό συνδυασμό των $v_1,\ldots, v_m$ είναι ο τετριμμένος: $0 v_1 + \cdots + 0 v_m = 0$.
Είδαμε παραδείγματα και είδαμε πώς μπορούμε να εξέγχουμε εάν κάποια δοσμένα διανύσματα του $\mathbb{R}^n$ είναι γραμμικώς ανεξάρτητα, βάζοντας τα στήλες σε ένα πίνακα και λύνοντας το ομογενές σύστημα.
Ορίσαμε την έννοια της βάσης ενός υπόχωρου: ένα σύνολο διανυσμάτων $\mathcal{B}$ είναι βάση ενός υπόχωρου $V$ εάν παράγει τον $V$ και είναι γραμμικώς ανεξάρτητο.
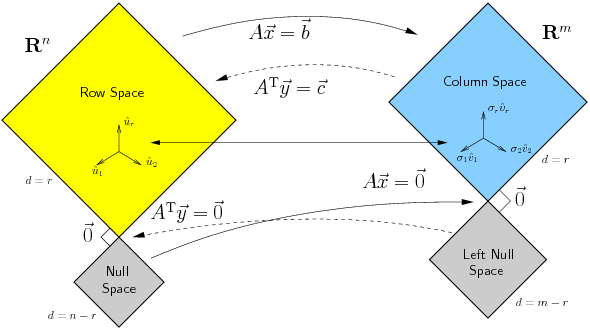
Ορίσαμε τους τέσσερις υπόχωρους που σχετίζονται με ένα πίνακα $A\in \mathbb{R}^{m\times n}$.
- Ο μηδενόχωρος $\mathcal{N}(A) \leq \mathbb{R}^n$ είναι το σύνολο λύσεων του ομογενούς συστήματος $A x = 0$.
- Ο χώρος στηλών $\mathcal{R}(A) \leq \mathbb{R}^m$ είναι ο χώρος που παράγουν οι στήλες του $A$.
- Ο χώρος γραμμών $\mathcal{R}(A^{\top}) \leq \mathbb{R}^n$ είναι ο χώρος που παράγουν οι γραμμές του $A$.
- Ο αριστερός μηδενόχωρος $\mathcal{N}(A^{\top}) \leq \mathbb{R}^m$.
Είδαμε πώς μπορουμε να υπολογίζουμε βάσεις για τους παραπάνω χώρους.
-
\(\)Είδαμε το Θεώρημα Αντικατάστασης: Έστω $V$ ένας υπόχωρος του $\mathbb{R}^n$. Εάν $A=\{u_1,\ \ldots, u_m\} \subseteq V$ είναι ένα γραμμικώς ανεξάρτητο σύνολο και $C = \{v_1,\ \ldots, v_k\}$ είναι ένα σύνολο που παράγει τον $V$, τότε
- $m\leq k$,
- Υπάρχουν δείκτες $i_1,\ \ldots, i_{k-m}$ τέτοιοι ώστε το σύνολο $\{u_1,\ \ldots, u_m, v_{i_1},\ \ldots, v_{i_{k-m}}\ \}$ παράγει τον $V$.
Από αυτό προκύπτει ότι κάθε βάση ενος υπόχωρου $V$ του $\mathbb{R}^n$ έχει το ίδιο πλήθος διανυσμάτων. Το πλήθος αυτό ονομάζεται διάσταση του $V$ και συμβολίζεται $\dim(V)$.
Επίσης είδαμε ότι οι παρακάτω προτάσεις είνια ισοδύναμες:
- Ο $V$ έχει διάσταση $m$
- Κάθε γραμμικώς ανεξάρτητο υποσύνλο $Α$ του $V$ με $m$ διανύσματα είναι βάση.
- Κάθε υποσύνλο $C$ του $V$ με $m$ διανύσματα, το οποίο παράγει τον $V$ είναι βάση.
Επομένως για να είναι ένα σύνολο διανυσμάτων, βάση του $V$ αρκεί να έχει το "σωστό" πλήθος στοιχείων και μία από τις δύο ιδιότητες που χαρακτηρίζουν μία βάση: είτε να είναι γραμμικώς ανεξάρτητο ή να παράγει. Σε αυτή την περίπτωση έχει απαραίτητα και τη δεύτερη ιδιότητα.
Είδαμε την κανονική βάση του $\mathbb{R}^n$ και παραδείγματα, όπου εφαρμόσαμε το Θεώρημα Αντικατάστασης για να επεκτείνουμε ένα γραμμικώς ανεξάρτητο σύνολο σε βάση.
Αν $A\in \mathbb{R}^{m\times n}$, τότε τα παραπάνω και όσα έχουμε δει για τους τέσσερις υόχωρους που σχτίζονται με τον πίκανα $A$, έχουμε:
- $\dim \mathcal{N}(A) = n-r$,
- $\dim \mathcal{R}(A) = r$,
- $\dim \mathcal{R}(A^{\top}) = r$,
- $\dim \mathcal{N}(A^{\top}) = m-r$,
όπου $r = \mathrm{rank}(A)$ είναι η τάξη του πίνακα $A$. Έτσι για κάθε πίνακα $A\in \mathbb{R}^{m\times n}$ ισχύει
\[ \dim \mathcal{N}(A) + \dim \mathcal{R}(A) = n. \]
Λύσαμε ασκήσεις.
-
\(\)Ορίσαμε την έννοια της γραμμικής απεικόνισης: Μία απεικόνιση $L : \mathbb{R}^n \longrightarrow \mathbb{R}^m$ ονομάζεται γραμμική εάν για κάθε $v,u\in \mathbb{R}^n$ και κάθε $\lambda\in \mathbb{R}$ ισχύει $L(\lambda v + u) = \lambda L(v) + L(u)$.
Είδαμε ότι κάθε γρ. απεικόνιση στέλνει το $0$ στο $0$ (δηλαδή $L(0)=0$). Είδαμε παραδείγματα.
Ορίσαμε τον πίνακα της γρ. απεικόνισης $L: \mathbb{R}^n \longrightarrow \mathbb{R}^m$, ως τον πίνακα $A\in \mathbb{R}^{m\times n}$ με την ιδιότητα $L(x) = Ax$ για κάθε $x\in\mathbb{R}$. Είδαμε ότι ο πίνακας με στήλες τα διανύσματα $L(e_1),\ldots, L(e_n)$ έχει αυτή την ιδιότητα και μάλιστα είναι μοναδικός. Συμβολίζουμε τον πίνακα της $L$ με $[L]$.
Ορίσαμε τον πυρήνα, $\mathbb{ker}(L)$ και την εικόνα, $\mathbb{im}(L)$, της $L$:
\[ \mathrm{ker}(L) = \left\{x\in \mathbb{R}^n\ :\ L(x) = 0\right\}, \]
\[ \mathrm{im}(L) = \left\{y\in \mathbb{R}^m\ :\ y = L(x)\ \mbox{ for some }\ x\in \mathbb{R}^n\right\}. \]
Είδαμε ότι $\mathrm{ker}(L) = \mathcal{N}([L])$ και $\mathrm{im}(L) = \mathcal{R}([L])$. Είδαμε ότι η $L$ είναι 1-1 αν και μόνο αν $\mathrm{ker}(L) = \{0\}$ (είναι τετριμμένος, όπως λέμε) και είναι επί αν και μόνο αν $\mathrm{im}(L) = \mathbb{R}^m$. Ισοδύναμα, η $L$ είναι 1-1 αν και μόνο αν $\dim(\mathrm{ker}(L)) = 0$ και είναι επί αν και μόνο αν $\dim(\mathrm{im}(L)) = m$.
Η σχέση $\dim \mathcal{N}([L]) + \dim \mathcal{R}([L]) = n$ μας δίνει άμεσα την αντίστοιχη σχέση για την $L$:
\[ \dim \mathrm{ker}(L) + \dim \mathrm{im}(L) = n. \]
-
\(\)Ορίσαμε τον πίνακα μίας γραμμικής απεικόνισης $L : \mathbb{R}^n \rightarrow \mathbb{R}^m$ ως προς οποιεσδήποτε βάσεις $\mathcal{A}=\{v_1,\ldots,v_n\}$ και $\mathcal{B}=\{u_1,\ldots,u_m\}$ των $\mathbb{R}^n$ και $\mathbb{R}^m$ αντίστοιχα: αν
\[ L(v_j) = a_{1j}\ u_1 + a_{2j}\ u_2 + \cdots + a_{mj}\ u_m,\ \ \ 1\leq j\leq n, \]
τότε $[L]_{\mathcal{A}}^{\mathcal{B}} = (a_{ij}) \in \mathbb{R}^{m\times n}$.
Είδαμε ότι η σύνθεση γραμμικών απεικονίσεων είναι γραμμική απεικόνιση και αν
\[ \mathbb{R}^n \stackrel{L}{\longrightarrow} \mathbb{R}^m \stackrel{T}{\longrightarrow} \mathbb{R}^p ,\]
και έχουμε τις βάσεις $\mathcal{A}, \mathcal{B}, \mathcal{C}$ για τους χώρους $\mathbb{R}^n, \mathbb{R}^m, \mathbb{R}^p$ αντίστοιχα, τότε
\[ [T\circ L]_{\mathcal{A}}^{\mathcal{C}} = [T]_{\mathcal{B}}^{\mathcal{C}} \cdot [L]_{\mathcal{A}}^{\mathcal{B}}.\]
Είδαμε τον πίνακα αλλαγής βάσης, που είναι ο πίνακας της ταυτοτικής απεικόνισης $\mathrm{id} : \mathbb{R}^n \rightarrow \mathbb{R}^n$ ως προς τις βάσεις που μας ενδιαφέρουν. Για παράδειγμα, αν $\mathcal{A} = \{v_1,\ldots, v_n\}$ είναι μία βάση του $\mathbb{R}^n$ και $\mathcal{E}$ είναι η κανονική βάση, τότε $\mathrm{id}(v_j) = v_j$ και ο πίνακας αλλαγής βάσης από την $\mathcal{A}$ στην $\mathcal{E}$, $[\mathrm{id}]_{\mathcal{A}}^{\mathcal{E}}$, είναι ο πίνακας με στήλες τα διανύσματα $v_1,\ldots, v_n$.
Γενικά, εάν η γραμμική απεικόνιση $L: \mathbb{R}^n \rightarrow \mathbb{R}^n$ είναι 1-1 και επί τότε είναι αντιστρέψιμη και έχουμε
\[ [L^{-1}]_{\mathcal{B}}^{\mathcal{A}} = \left([L]_{\mathcal{A}}^{\mathcal{B}}\right)^{-1}.\]
Εφαρμόζοντας το για την ταυτοτική απεικόνιση, έχουμε
\[ [\mathrm{id}]_{\mathcal{E}}^{\mathcal{A}} = ([\mathrm{id}^{-1}]_{\mathcal{A}}^{\mathcal{E}})^{-1} = ([\mathrm{id}]_{\mathcal{A}}^{\mathcal{E}})^{-1}.\]
Είδαμε τον ορισμό της ιδιοτιμής $\lambda\in \mathbb{R}$ ενός πίνακα $A\in \mathbb{R}^{n\times n}$ και του αντίστοιχου ιδιόχωρου $V_{\lambda} = \mathcal{N}(A-\lambda I)$.
-
\(\)Ορίσαμε το χαρακτηριστικό πολυώνυμο ενός πίνακα $A\in \mathbb{R}^{n\times n}$ ως $\chi_A(x) = \mathrm{det}(A- x I)$ και είδαμε ότι οι ρίζες του πολυωνύμου αυτού είναι οι ιδιοτιμές του πίνακα $A$. Ορίσαμε επίσης τον ιδιόχωρο που αντιστοιχεί σε μία ιδιοτιμή $\lambda$ ως τον υπόχωρο $V_{\lambda} = \mathcal{N}(A - \lambda I) = \{v\in \mathbb{R}^n\ :\ A v = \lambda v \}$. Από τον ορισμό της ιδιοτιμής έχουμε ότι $V_{\lambda} \neq \{0\}$, δηλαδή $\dim V_{\lambda} \geq 1$.
Αν $\lambda_1,\ldots, \lambda_k\in \mathbb{R}$ είναι οι (πραγματικές) ιδιοτιμές του πίνακα $A$, τότε το χαρακτηριστικό πολυώνυμο παραγοντοποιείται ως $\chi_A(x) = (-1)^n (x-\lambda_1)^{n_1} \cdots (x-\lambda_k)^{n_k}\ g(x)$, όπου $ g(x)$ είναι ένα πολυώνυμο βαθμού $n - (n_1+\cdots+n_k)$, το οποίο δεν έχει πραγματικές ρίζες. Ο αριθμός $n_i$ ονομάζεται αλγεβρική πολλαπλότητα της ιδιοτιμής $\lambda_i$. Η διάσταση $m_i = \dim V_{\lambda_i}$ ονομάζεται γεωμετρική πολλαπλότητα της ιδιοτιμής $\lambda_i$. Για κάθε πίνακα $A$ και κάθε ιδιοτιμή $\lambda$ ισχύει $n_i \geq m_i$ (η αλγεβρική πολλαπλότητα είναι μεγαλύτερη ή ίση της γεωμετρικής πολλαπλότητας).
Δύο πίνακες $A, B\in \mathbb{R}^{n\times n}$ ονομάζονται όμοιοι εάν υπάρχει αντιστρέψιμος πίνακας $P\in \mathbb{R}^{n\times n}$ τέτοιος ώστε $B = P^{-1} A P$. Είδαμε ότι αν $L : \mathbb{R}^n \rightarrow \mathbb{R}^n$ είναι γραμμική και $\mathcal{B}$ είναι μία βάση του $\mathbb{R}^n$, τότε οι πίνακες $B = [L]_{\mathcal{B}}^{\mathcal{E}}$ και $A = [L]$ είναι όμοιοι και ειδικότερα $B = P^{-1} A P$, όπου $P$ είναι ο πίνακας με στήλες τα διανύσματα της βάσης $\mathcal{B}$.
Ένας πίνακας $A$ ονομάζεται διαγωνιοποιήσιμος εάν υπάρχει διαγώνιος πίνακας $D$ και αντιστρέψιμος πίνακας $P$ τέτοιοι ώστε $A = P^{-1} D P$. Ένας πίνακας $A\in\mathbb{R}^{n\times n}$ είναι διαγωνιοποιήσιμος αν και μόνο αν υπάρχει μία βάση $\mathcal{B}$ του $\mathbb{R}^n$ αποτελούμενη από ιδιοδιανύσματα του $A$. Είδαμε ότι η συνθήκη αυτή ικανοποιείται αν και μόνο αν $m_1+\cdots m_k = n$, όπου $\lambda_1,\ldots, \lambda_k$ είναι οι διακεκριμένες ιδιοτιμές του $A$ και $m_1,\ldots, m_k$ είναι οι αντίστοιχες γεωμετρικές πολλαπλότητες. Παρατηρήσαμε ότι στην περίπτωση που ο πίνακας είναι διαγωνιοποιήσιμος, $m_i = n_i$ για κάθε ιδιοτιμή. Επίσης, παρατηρήσαμε ότι αν το χαρακτηριστικό πολυώνυμο αναλύεται ως $\chi_A(x) = (x-\lambda_1)\cdots (x-\lambda_n)$, τότε $1\leq m_i \leq n_i = 1$, οπότε $n = m_1+\cdots+m_n$ και ο πίνακας είναι διανωνιοποιήσιμος. Είδαμε παραδείγματα.
-
\(\)Είδαμε το Θεώρημα των Cayley-Hamilton: Αν $A\in\mathbb{R}^{n\times n}$ και $\chi_A(x)$ είναι το χαρακτηριστικό του πολυώνυμο, τότε $\chi_A(A) = 0$.
Ορίσαμε το standard εσωτερικό γινόμενο δύο διανυσμάτων $v = (v_1,\ldots, v_n)$ και $u=(u_1,\ldots, u_n)$ ως
\[ \langle v, u\rangle = v_1 u_1 + \cdots + v_n u_n.\]
Αποδείξαμε βασικές ιδιότητες.
Δύο διανύσματα $v, u$ θα λέγονται ορθογώνια (ή κάθετα μεταξύ τους) εάν $\langle v, u\rangle = 0$.
Ορίσαμε το μήκος ενός διανύσματος $v=(v_1,\ldots, v_n)$ ως
\[ \| v\| = \sqrt{\langle v, v \rangle} = \sqrt{v_1^2 + \cdots + v_n^2}. \]
Δείξαμε την ανισότητα Cauchy-Schwarz
\[ | \langle v, u\rangle | \leq \|v\| \|u\| \]
και την τριγωνική ανισότητα
\[ \|v + u\| \leq \|v\| + \|u\|.\]
-
\(\)Για δεδομένο υπόχωρο $U\leq \mathbb{R}^n$ ορίσαμε το ορθογώνιο συμπλήρωμα ως
\[ U^{\perp} = \left\{ v\in\mathbb{R}^n\ :\ \langle v, u\rangle = 0\ \mbox{ for every }\ u\in U\right\}. \]
Δείξαμε ότι $\dim U + \dim U^{\perp} = n$.
Είδαμε το αλγόριθμο ορθοκανονικοποίησης των Gram-Schmidt. Παρατηρήσαμε ότι εάν $u_,\ldots, u_k$ είναι μία βάση του $U$ και την συμπληρώσουμε (με οποιοδήποτε τρόπο) σε μία βάση $\{u_1\,\ldots, u_k, u_{k+1}\ ,\ldots, u_n\ \}$ του $\mathbb{R}^n$ και στη συνέχεια ορθοκανονικοποιήσουμε τη βάση αυτή, θα πάρουμε μία ορθοκανονική βάση $\{u_1^*, \ldots, u_n^*\}$ με την ιδιότητα:
\[ U = \mathrm{Span}(\{u_1^*,\ldots, u_k^*\}) \ \ \ U^{\perp} = \mathrm{Span}(\{u_{k+1}^*,\ldots, u_n^*\}).\]
Μιλήσαμε για προβολή διανύσματος σε υπόχωρο και είδαμε τη μέθοδο ελαχίστων τετραγώνων.
-
\(\)Λύσαμε ασκήσεις.
-
-
-