Θεωρία Δακτυλίων και Modules

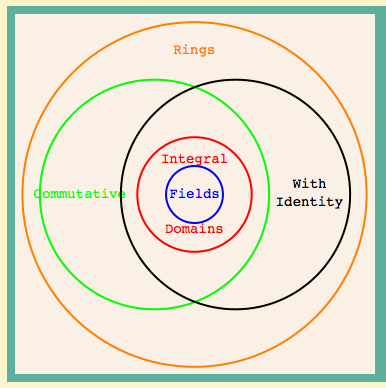
Ώρες Μαθημάτων: Δευτέρα, 11-13 και Τετάρτη 11-13

Ώρες Γραφείου: Δευτέρα 13-14 και Τετάρτη 13-14

Εξεταστικό: --- Ασκήσεις 2/10

---- Πρόοδος στο πρώτο μέρος του μαθήματος, 3/10

----- Τελική εξέταση 5/10

------ Διαλέξεις. Οι διαλέξεις είναι προαιρετικές. Κάθε φοιτητής μπορεί να δώσει έως δύο ωριαίες,περίπου, διαλέξεις.

Η προετοιμασία του φοιτητή θα γίνει με τη δική μου βοήθεια. Μία διάλεξη στο πρώτο μέρος και μία στο δεύτερο μέρος του μαθήματος. Για κάθε διάλεξη το άριστα θα είναι 1 μονάδα.

------ Η ύλη των διαλέξεων θα είναι μέρος του μαθήματος.

------- Εννοείται ότι η βάση είναι το 5 και το άριστα το, μεγαλύτερο ή ίσο του 10.

ΠΡΟΣΟΧΗ: ΟΙ ΑΣΚΗΣΕΙΣ ΘΑ ΓΙΝΟΝΤΑΙ ΔΕΥΤΕΡΑ ΚΑΙ ΤΕΤΑΡΤΗ 13-14

ΠΑΡΑΚΑΛΩ ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΝΑ ΓΡΑΦΟΝΤΑΙ ΣΕ ΞΕΧΩΡΙΣΤΟ ΦΥΛΛΟ Η ΚΑΘΕΜΙΑ. Να παραδίσονται με συνδετήρα.

Μην κόβετε φύλλα από τετράδιο SPIRAL.

$forum icon$

Forum

Announcements Forum
$resource icon$

File

ΛΥΣΕΣ ΑΣΚΗΣΕΩΝ ΦΥΛΛΑΔΙΟ 4ο File

25 September - 1 October

Διάλεξη 1η, Ορισμός και ιδιότητες των δακτυλίων, παραδείγματα, μεταθετικοί δακτύλιοι με μοναδιαίο, διαιρέτες του μηδενός, ακέραιες περιοχές μονάδες

μιάς ακέραιας περιοχής.

2η Διάλεξη, Υποδακτύλιοι, απεικονίσεις δακτυλίων, ιδεώδη, δακτύλιος πηλίκο, πρώτο θεώρημα ισομορφίας.

Files: 2

Progress: 0 / 0

2 October - 8 October

3η Διάλεξη, Δακτύλιοι και διαιρετότητα, Μονάδες, συνεταιρικά στοιχεία, Ευκλείδειες περιοχές,περιοχές κυρίων ιδεωδών.

4η Διάλεξη, ο Δακτύλιος των πολυωνύμων R[X], αλγόριθμος διαίρεσης, κριτήρια αναγωγισιμότητας, περιοχές μονοσήμαντης ανάλυσης,

πράξεις ιδεωδών και το θεώρημα υπολοίπων του Κινέζου.

Η ύλη των πρώτων δύο εβδομάδων αποτελεί σύντομη επανάληψη του περιεχομένου του μαθήματος ΑΛΓΕΒΡΑ ΙΙ

Files: 2

Progress: 0 / 0

9 October - 15 October

Διάλεξη 5η

Δακτύλιοι και περιοχές της Noether.

Κάθε Π.Κ.Ι. είναι περιοχή της Noether, οπότε και κάθε Ευκλείδεια περιοχή.

Κάθε περιοχή της Noether είναι και περιοχή ανάλυσης (Π.Α.)

Διάλεξη 6η

Το θεώρημα βάσης του Hilbert, Αν R περιοχή της Noether, τότε και η R[X] επίσης περιοχή της Noether.

Επομένως και R[X_1,X_2,...,X_n] επίσης περιοχή της Noether. Ιδιαίτερα, Ζ[Χ_1,Χ_2,...,,Χ_n] και Κ[Χ_1,Χ_2, ..., Χ_n], K σώμα.

Files: 2

Progress: 0 / 0

16 October - 22 October

7η Διάλεξη, Διάσταση του Krull, Δακτύλιοι του Artin,και χαρακτηρισμός τους.

Εισαγωγή στις διοφαντικές εξισώσεις.

8η Διάλεξη, παραδείγματα επίλυσης διοφαντικών εξισώσεων. Ιστορικά στοιχεία σχετικά με την με την

προσπάθεια επίλυσης της Εικασίας Fermat και τις περιοχές μονοσήμαντης ανάλυσης.

File: 1

Progress: 0 / 0

9η Διάλεξη, Ριζικό ιδεώδους. το ριζικό πρώτων ιδωδών ταυτίζεται με το ιδεώδες .Παραδείγμαστα, ριζικό ιδεώδους σε Π.Μ.Α., Spec(R), maxSpec(R), κάθε (γνήσιο0 ιδεώδες του R περιέχεται σε κάποιο maximal. Πολλαπλασιαστικά κλειστό υποσύνολο δακτυλίου, παραδείγματα.

10η Διάλεξη. Σημαντική πρόταση για την απόδειξη ότι το Rad(A) είναι ίσο προσ την τομή των πρώτων ιδεωδών που περιέχουν το Α.. Ριζικό του Jacobson και η πρόταση χαρακτηρισμού του. Θεώρημα αποφυγής πρώτων ιδεωδών.

File: 1

Progress: 0 / 0

30 October - 5 November

11η Διάλεξη, Επέκταση και συστολή ιδεωδών, πηλίκο ιδεωδών , ιδιαίτερα μηδενιστής (annihilator) ιδεώδους

τοπικοί δακτύλιοι, χαρακτηρισμός αυτών και μηδενοδύναμα (nilpotent) στοιχεία δακτυλίου.

( Σημείωση: Η άσκηση 5 του 5ου φυλλαδίου μπορεί να μείνει να εξεταστεί μαζί με τις ασκήσεις του 6ου Φυλλαδίου.)

12η Διάλεξη, Μεταθετική Άλγεβρα και Αλγεβρική Γεωμετρία. Αναφορά στην προβληματική του θέματος. Ορισμός του

αλγεβρικού συνόλου και βασικές ιδιότητες αυτού. Πότε ένα πολυωνυμικό σύσημα εξισώσεων (με συντελεστές από κάποιο αλγεβρικά κλειστό σώμα,

π.χ. το C, ) έχει λύση? Στόχος μας το Nullstellensatz του Hilbert.

6 November - 12 November

13η Διάλεξη, Αναλυτική παρουσίαση των συνεπειών του Hilbert Nullstellensatz, όσον αφορά στα ερωτήματα που θέσαμε στην αρχή, όπως πότε υπάρχει λύση

του συστήματος πότε δύο συστήματα είναι "ισοδύναμα" ( 'εχουν ακριβώς το ίδιο σύνολο λύσεων).

14η Διάλεξη, Ορισμός τοπολογικού χώρου, ανοιχτά ,κλειστά σύνολα, επαγώμενη τοπολογία σε υποσύνολα του χώρου,

Η τοπολογία του Zariski, Η τοπολογική έκφραση του Nullstellensatz, ανάγωγα αλγεβρικά σύνολα, τοπολογικοί χώροι της Noether,

ανάλυση αλγεβρικών συνόλων σε ένωση ανάγωγων συνιστωσών.

ΣΗΜΕΙΩΣΗ: Εδώ κλείνει, προς το παρόν, η" Εσαγωγή στην Αλγεβρική Γεωμετρία". Μαζί με το 7ο φυλλάδιο ασκήσεων κλείνει και

η ύλη της προόδου.

Από την Δευτέρα 13η Νοεμβρίου, συνεχίζουμε με το δεύτερο μέρος του μαθήματος που είναι η θεωρία των modules.

Files: 2

Progress: 0 / 0

13 November - 19 November

15η Διάλεξη,

Εισαγωγή στη θεωρία των module. Βασικές έννοιες, ορισμοί και πρώτεσ ιδιότητεσ παραδείγματα. Υπο- modules, moduleς πηλίκο,

ομομορφισμοί μεταξύ των modules, θεωρήματα ισομορφίας. ευθέα αθροίσματα από modules. Γιατί μελετούμε τα modules;

(4 σημαντικές απαντήσεις)

16η Διάλεξη, Ελεύθερα modules, ( γραμματική ανεξαρτησία, βάσεις, παραδείγματα) R-modules και Κ-διανυσματικοί χώροι,. Σύγκριση και μερικές "παθογένειες"

των R-modules σε σχέση με τους Κ-διανυσματυκούς χώρους.

Files: 3

Progress: 0 / 0

20 November - 26 November

Διάέξη 17η, Το θεώρημα για παπερασμένα R-modules και δύο από τα πορίσματα του (Λήμμα του ΝΑΚΑΥΑΜΑ)

Διάλεξη 18η, Γενίκευση του λήμματος του NAKAYAMA και εφαρμογή στους τοπικούς δακτυλίους.

Όλες οι βάσεις ενός ελεύθερου R-module έχουν τον ίδιο πληθάριθμο.(Βαθμός, διάσταση του ελεύθερου R-module)

File: 1 Assignment: 1

Progress: 0 / 0

27 November - 3 December

Διάλεξη Όταν R είναι Π.Κ.Ι. τότε κάθε υποmodule ενός ελεύθερου module με πεπερασμενο rank είναι επίσης ελεύθερο με ρανκ μικρότερο ή ίσο του rank του αρχικού.

modules στρέψεως, modules ελεύθερα στρέψεως, Αν R μεταθετικός με μοναδιαίο τότε Μ_tor είναι υπο-module του R. αν Rακέραια περιοχή, τότε Μ/Μ_tor

είναι module ελεύθερο στρέψεως Ελεύθερο στρέψεως δεν είναι οπωσδήποτε και ελεύθερο R-module,

Διάλεξη, Αν R Π.Κ.Ι. και Μ πεπ. παραγ. και ελεύθερο στρέψεως , τότε Μ κατ ανάγκη ελεύθερο.

Αν R Π.Κ.Ι και Μ πεπ. παρ. τότε Μ=Μ_tor ευθύ άθροισμα Μ_free.

ELEMENTARTEILERSATZ και διατύπωση των θεωρημάτων ΑΝΑΛΥΣΗΣ στην περίπτωση που ο R είναι Π.Κ

Files: 2

Progress: 0 / 0

4 December - 10 December

Διάλεξη τοπικοποίηση, ορισμός και παραδείγματα. Ομομορφισμοί δακτυλίων με την συνθήκη g(s) μονάδα του R_2

"παραγοντοποιούνται" (factor through) της τοπικοποίησης. h: S^(-1)R_1 στο R_2 τ.ώστε g=hof.

Πότε η απεικόνιση h είναι ισομορφισμός.

Διάλεξη Τοπικοποίηση στα R modules. Επαγώμενος ομομορφισμός από τα modules στις τοπικοποιήσεις.

Διατηρεί την ακρίβεια μιας μικρής ακριβούς ακολουθίας. Τοπικές ιδιότητες και παραδείγματα.

Εισαγωγή στην ακεραιότητα.

Files: 2

Progress: 0 / 0

11 December - 17 December

Διάλεξη Ιστορική εισαγωγή στην έννοια της ακεραιότητας. Ορισμός και παραδείγματα. Το Θεώρημα χαρακτηρισμών της ακεραιότητας. Ακέραια θήκη επέκτασης δακτυλίων.

ακέραια κλειστότητα σε επέκταση δακτυλίων και ειδικά για ακέραια περιοχή. Ιδιότητα μεταβατικότητας τησ ακεραιότητας. Η έννοια "μεταφέρεται" σε δακτύλους πηλίκο κα στην

τοποκοποίηση. Η ακέραια κλειστότητα είναι τοπική ιδιότητα.

Διάλεξη Δακτύλιοι εκτίμησης. Απόδειξη ότι είναι τοπικοί δακτύλιοι.παραδείγματα. Διακριτές εκτιμήσεις ενός σώματος. Αν R ακέραια περιοχή ,ορίζεται ο δακτύλιος διακριτής ακτίμησης (D.V.R.). Παραδείγματα.

18 December - 24 December

Διάλεξη, Κλασματικά ιδεώδη ακέραιας περιοχής, κύρια κλασματικά ιδεώδη, αντιστρέψιμα κλασματικά ιδεώδη.

όλα τα κύρια κλασματικά ιδεώδη είναι αντιστρέψιμα, το σύνολο όλων των αντιστρέψιμων αποτελεί (αβελιανή) πολλαπλασιαστική ομάδα με μοναδιαίο στοιχείο το R.

το σύνολο των κύριων κλασματικών ιδεωδών αποτελεί υποομάδα της ομάδας όλων των αντιστρέψιμων κλασματικών ιδεωδών του R. η ομάδα πηλίκο λέγεται ομάδα κλάσεων ιδεωδών της ακεραίας περιοχής R.

Διάλεξη, Πρόταση: Αν R περιοχή R όχι σώμα τότε (ο R είναι DVR) τότε και μόνο τότε όταν ( κάθε κλασματικό ιδεώδες του R, διάφορο του μηδενικού, είναι αντιστρέψιμο)

Περιοχές Dedekind: Ορισμός Μία ακεραια περιοχή R λέγεται περιοχή Dedekind ότανν

1. Είναι περιοχή της Noether

2. Είναι ακέραια κλειστή

3. Έχει Krull dimension 1

Πρόταση: Κάθε Π.Κ.Ι. είναι και περιοχή Dedekind.

Ισοδύναμοι χαρακτηρισμοί μιας περιοχής Dedekind.

Ο δακτύλιος των ακεραίων αλγεβρικών αριθμών ενός αλγεβρικού σώματος αριθμών

είναι περιοχή Dedekind.

ΣΩΣΤΗ !!!! επίλυση της διοφαντικής εξίσωσης 2Υ^3=Χ^2+5

-

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++-

++++++++++++++-

++++++++++++++++++++++++++++++++++++++++++++++++

Ευχαριστώ Γ.Α.

ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΕ ΟΛΟΥΣ ΟΣΟΥΣ ΠΑΡΟΥΝ ΜΕΡΟΣ ΣΤΗΝ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ!

ΟΛΑ ΤΑ ΩΡΑΙΑ ΠΡΑΓΜΑΤΑ ΚΑΠΟΤΕ ΤΕΛΕΙΩΝΟΥΝ
ΚΑΙΡΟΣ ΓΙΑ ΑΛΛΑ ΤΑΞΕΙΔΙΑ!

ΓΙΑΝΝΗΣ Α> ΑΝΤΩΝΙΑΔΗΣ

Files: 5

Progress: 0 / 0

Weekly outline

Θεωρία Δακτυλίων και Modules