Για την πρόταση που μας είπατε στο μάθημα(την διορθώσατε στο φόρουμ του μαθήματος)έχω βρει μια συνάρτηση που νομίζω πως είναι ομοιόμορφα συνεχής στο R αλλά δεν έχει φραγμένη παράγωγο στο R.Ορίζω την f(x)=(x^2)*(sin(1/x^2)) για x!=0 και f(0)=0.Αναφέραμε την εξής πρόταση αν τα όρια της f(x) στο συν πλην άπειρο υπάρχουν και είναι πεπερασμένα αν η f είναι συνεχής στο R--->f ομοιόμορφα συνεχής στο R.Επομένως,η συγκεκριμένη συνάρτηση είναι ομοιόμορφα συνεχής στο R καθώς είναι συνεχής στο R(είναι συνεχής στο R* ως γινόμενο-σύνθεση συνεχών συναρτήσεων και στο 0 αφού το όριο είναι ίσο με 0)και επιπλέον τα όρια στο -00,+00 είναι ίσα με 1eR(limy--->0 (siny/y)=1).Επιπλέον,είναι παραγωγίσιμη σε όλο το R* ως γινόμενο-σύνθεση παραγωγίσιμων συναρτήσεων και ειδικά στο 0 limx-->0 (f(x)-f(0))/(x-0)=0=f'(0).Ωστόσο,δεν έχει φραγμένη παράγωγο η συγκεκριμένη f...Στο 0 η παράγωγος ενώ υπάρχει δεν είναι συνεχής αν κοιτάξουμε την παράγωγο για χ πολύ κοντά στο 0 απειρίζεται(κάνω λάθος;;;).
Συζητήσεις για το μάθημα
f:R→R δεν είναι φραγμένη τότε η f δεν είναι ομοιόμορφα συνεχής στο R;;
Σωστό είναι το παράδειγμά σας. Η συνάρτηση είναι παραγωγίσιμη παντού και η παράγωγος κοντά στο 0 παίρνει οσοδήποτε μεγάλες τιμές. Η παράγωγος στο 0 υπάρχει και είναι 0 και η παράγωγος είναι ασυνεχής στο 0. Τα όρια στο \(\pm\infty\) υπάρχουν για τους λόγους που περιγράφετε και άρα η συνάρτηση είναι ομοιόμορφα συνεχής στο \(\RR\), παραγωγίσιμη και με μη φραγμένη παράγωγο.
Θα ήθελα να σας δώσω και μια ακόμη λύση και θυμηθείτε αυτό που σας είχα πει στο μάθημα: αν ψάχνετε να βρείτε ένα παράδειγμα (συνάρτηση, ακολουθία, δεν έχει ιδιαίτερη σημασία) και ψάχνετε το παράδειγμά σας ανάμεσα σε συναρτήσεις που έχουν κάποιο τύπο τότε είναι σα να έχετε δέσει μόνοι σας τα χέρια σας.
Πάρτε λοιπόν την παρακάτω συνάρτηση \(\phi(x)\):
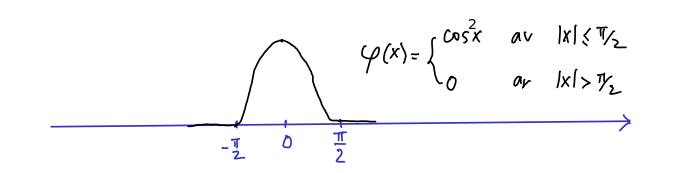
Η συνάρτηση αυτή είναι παντού παραγωγίσιμη. Τα μόνα σημεία που χρειάζονται έλεγχο είναι τα \(\pm\pi/2\) όμως εκεί υπάρχουν όλες οι πλευρικές παράγωγοι και είναι 0, άρα υπάρχει και εκεί η παράγωγος.
Φτιάχνουμε τώρα το παράδειγμά μας μέσω της \(\phi(x)\) ως εξής:
\[ f(x) = \sum_{n=1}^\infty \frac{1}{n} \phi(n^{10} (x-100 n)).\]
Η συνάρτηση μοιάζει κάπως έτσι:

Έχει άπειρα αντίγραφα της \(\phi(x)\), ένα σε κάθε εκατοντάδα (για να είμαστε σίγουροι ότι δεν ακουμπάνε μεταξύ τους). Το ύψος τους τείνει στο 0 όσο πάμε στο \(\infty\) (λόγω του παράγοντα \(1/n\) μπροστά από τα \(\phi\) μέσα στο άθροισμα) και άρα η συνάρτηση μας έχει όριο 0 στα άπειρα (αριστερά δεν υπάρχει κανένα θέμα γιατί είναι ταυτοτικά 0) είναι παντού συνεχής και άρα ομοιόμορφα συνεχής στο \(\RR\).
Όμως τα αντίγραφα της \(\phi\) που χρησιμοποιούμε είναι τα \(\phi(n^{10}(x-100n))\). Αυτά είναι όντως "κεντραρισμένα" στο \(100 n\) (γι' αυτό γράφουμε \((x-100n)\)) αλλά, λόγω του παράγοντα \(n^{10}\) μπροστά από το \((x-100n)\) το αντίγραφο της \(\phi\) που τοποθετούμε στη θέση \(100n\) έχει "στενέψει" κατά ένα παράγοντα \(n^{10}\), εκτείνεται δηλ. από τη θέση \(100 n - \frac{\pi}{2 n^{10}}\) έως τη θέση \(100 n + \frac{\pi}{2 n^{10}}\). Αυτό το στένεμα έχει ως αποτέλεσμα να μεγαλώνει πολύ η παράγωγος της συνάρτησης εκεί, πολύ περισσότερο απ' ό,τι μικραίνει λόγω του παράγοντα \(1/n\) μπροστά από το \(\phi\). Πράγματι η σειρά που μας δίνει την \(f\) παραπάνω μπορεί να παραγωγιστεί κατά όρους αφού για κάθε \(x\) υπάρχει μόνο ένας όρος της σειράς που δεν είναι 0. Παίρνουμε έτσι
\[ f'(x) = \sum_{n=1}^\infty \frac{1}{n} n^{10} \phi'(n^{10}(x-100n)) = \sum_{n=1}^\infty n^9 \phi'(n^{10}(x-100n)).\]
Εύκολα μπορεί κανείς να βρει τώρα μια ακολουθία σημείων \(x_n\), από ένα σε κάθε "αντίγραφο" της \(\phi\), τέτοια ώστε \(f'(x_n) \to \infty\), δείχνοντας έτσι ότι η \(f'\) δεν είναι φραγμένη. Μπορείτε για παράδειγμα να πάρετε ένα σημείο στο μέσο του διαστήματος
\[ [100n - \frac{\pi}{2 n^{10}}, 100n] \]
ή, ακόμη καλύτερα, μπορείτε να χρησιμοποιήσετε το Θεώρημα Μέσης Τιμής και να πείτε ότι αφού στα άκρα του διαστήματος αυτού η συνάρτησή μας παίρνει τιμές \(1/n\) και 0 θα πρέπει να υπάρχει ένα σημείο \(x_n\) μέσα σε αυτό το διάστημα όπου
\[ f'(x_n) = \frac{\frac{1}{n}-0}{ \frac{\pi}{2 n^{10}}} = 2 n^9. \]