Weekly outline

  • General

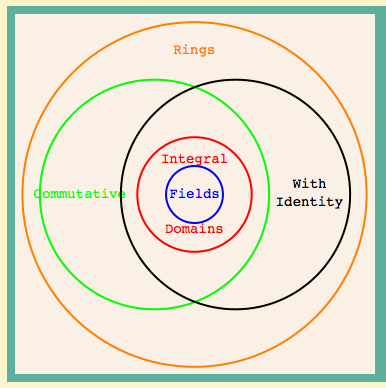
            Θεωρία Δακτυλίων και Modules 

                                       

    Ώρες Μαθημάτων:   Δευτέρα, 11-13 και Τετάρτη 11-13

    Ώρες Γραφείου:  Δευτέρα 13-14 και Τετάρτη 13-14

    Εξεταστικό: --- Ασκήσεις     2/10

                          ---- Πρόοδος στο πρώτο μέρος του μαθήματος, 3/10

                          ----- Τελική εξέταση            5/10

                          ------ Διαλέξεις. Οι διαλέξεις είναι προαιρετικές. Κάθε φοιτητής μπορεί να δώσει έως δύο ωριαίες,περίπου, διαλέξεις.

                                    Η προετοιμασία του φοιτητή θα γίνει με τη δική μου βοήθεια.  Μία διάλεξη στο πρώτο μέρος και μία στο δεύτερο μέρος του                                                μαθήματος. Για κάθε διάλεξη το άριστα θα είναι 1 μονάδα.

                       ------  Η ύλη των διαλέξεων θα είναι μέρος του μαθήματος.

                      ------- Εννοείται  ότι η βάση είναι  το 5 και το άριστα  το, μεγαλύτερο ή ίσο του 10.

                   ΠΡΟΣΟΧΗ: ΟΙ ΑΣΚΗΣΕΙΣ ΘΑ ΓΙΝΟΝΤΑΙ ΔΕΥΤΕΡΑ ΚΑΙ ΤΕΤΑΡΤΗ 13-14

      ΠΑΡΑΚΑΛΩ ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΝΑ ΓΡΑΦΟΝΤΑΙ ΣΕ ΞΕΧΩΡΙΣΤΟ ΦΥΛΛΟ Η ΚΑΘΕΜΙΑ. Να παραδίσονται με συνδετήρα.

    Μην κόβετε φύλλα από τετράδιο SPIRAL.

                         

  • 18 December - 24 December

      

      Διάλεξη, Κλασματικά ιδεώδη ακέραιας περιοχής, κύρια κλασματικά ιδεώδη, αντιστρέψιμα κλασματικά ιδεώδη. 

     όλα τα κύρια κλασματικά ιδεώδη είναι αντιστρέψιμα, το σύνολο όλων των αντιστρέψιμων αποτελεί (αβελιανή) πολλαπλασιαστική ομάδα με μοναδιαίο στοιχείο το R.

     το σύνολο των κύριων κλασματικών ιδεωδών αποτελεί υποομάδα της ομάδας όλων των αντιστρέψιμων κλασματικών ιδεωδών του R. η ομάδα πηλίκο λέγεται ομάδα κλάσεων ιδεωδών της ακεραίας περιοχής R.

    Διάλεξη, Πρόταση: Αν R  περιοχή R όχι σώμα τότε (ο R είναι DVR)  τότε και μόνο τότε όταν ( κάθε κλασματικό ιδεώδες του R, διάφορο του μηδενικού, είναι αντιστρέψιμο)

      Περιοχές Dedekind: Ορισμός Μία ακεραια περιοχή R λέγεται περιοχή Dedekind  ότανν  

       1. Είναι περιοχή της Noether

        2. Είναι ακέραια κλειστή

         3.  Έχει Krull dimension 1

     Πρόταση: Κάθε Π.Κ.Ι. είναι και περιοχή  Dedekind.

     Ισοδύναμοι χαρακτηρισμοί μιας περιοχής Dedekind.

      Ο δακτύλιος των ακεραίων αλγεβρικών αριθμών ενός αλγεβρικού σώματος αριθμών

    είναι περιοχή Dedekind.

     ΣΩΣΤΗ !!!! επίλυση της διοφαντικής εξίσωσης  2Υ^3=Χ^2+5

    -

    ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++-

    ++++++++++++++-

    ++++++++++++++++++++++++++++++++++++++++++++++++